.
Introduction
The "paradox" of the twins dates from Einstein's first paper on relativity (Einstein, 1905), but he only alluded there to a "peculiar consequence" of his theory which didn't involve a re-uniting of twins, just distant clocks becoming un-synchronized by one's acceleration. The situation doesn't properly belong in a discussion of Special Relativity, which is "special" because it excludes the consideration of accelerations, and Einstein had yet to fully explore the relativistic implications of acceleration; but in subsequent investigations of acceleration and gravitation he and others have succeeded in accounting for the "peculiarity." It was coined a "twin paradox" by Paul Langevin (1911) and explicitly tied to the effect of inertial acceleration. Einstein later (1918) discussed it in terms of gravitation.
Numerous experiments have confirmed that both inertial accelerations and gravitational effects produce a dilation, or slowing of a body's clock, which unlike the relationship between bodies in relative uniform motion, is absolute -- i.e., agreed upon from any frame of reference (Rossi, Hall 1941; Pound, Rebka Jr. 1959; Hafele, Keating 1972; Bailey, et al 1977; Botermann, et al 2014). The plausibility of a "twin effect", whereby people who undergo prolonged and intense accelerations can age significantly less than those who don't, has thus acquired a solid experimental foundation.
The Conundrum
Simply stated, the basis of the alleged paradox is this: If a twin accelerates toward a distant star-system, decelerates at the destination, accelerates back toward earth, then decelerates for a reunion with the stay-at-home twin, the traveling twin will have aged less than the stay-at-home. (Some theorists have tried to attribute the effect not to the accelerations but to the traveling twin's change of coordinate systems in the return (Laue 1913), but I'll demonstrate below that this is not the case.)
A thought-experiment with twins that attributes the "peculiarity" of time dilation to acceleration works fine when the traveling twin is constantly accelerating or decelerating, as it can fully account for the differences in age at the reunion. But if the traveling twin spends any time during the journey moving uniformly, the principle of Special Relativity applies, and each twin will regard the other's clock as being only relatively dilated during those periods. A time period spent in relative motion between accelerations introduces this conundrum: If each twin has been observing the other's clock moving relatively slower during any part of their separation, how can their clocks agree on that part of the journey, how can the mutual observation of the other's relative dilations be resolved when they are reunited?
A Visualization
The spacetime diagram used below to visualize the Twin problem differs from the conventional Minkowski diagram (1908) in that it plots a world-line (the motion of a body in spacetime) of an observed body according to its own clock rather than the clock of the observer.(Characteristically, the Minkowski diagram portrays a ray of light as moving in spacetime at 1 light-second per second (hence the "light-cones"), but according to Relativity light moves at a relative zero seconds per light-second, while the observer records the motion in 1 second.) I've discussed what I've called the flaw in the Minkowski construction elsewhere (Arnold 2015), but I'll use the alternative here without comparison and argumentation, and simply proceed on the basis of its evident utility.
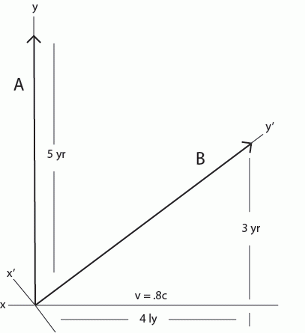
A diagram (figure 1) conforming to Special Relativity and the Lorentz transformations, and treating time as relative, provides a heuristic representation by means of which the relativistic relationship can be visualized as Minkowski originally intended, so that "physical laws might find their most perfect expression" (Minkowski 1908, p.76 ).
The x-axis in figure 1 represents space calibrated in light-years (ly), while its perpendicular, the y-axis, represents time calibrated in years (yr) -- both according to observer A, who is considered to be at rest in space and moving in time along the y-axis. Vector B represents a body in motion relative to A. Body B moves from the vicinity of A at a velocity which will take it 4 ly in 5 yr according to A with an elapsed time of 3 yr on B's clock. The x' and y' axes represent B's coordinate system.
figure 1(Note: You can view every article as one long page if you sign up as an Advocate Member, or higher).